In the last few days, I get an increasing number of people coming up to me in the street and saying “But Stavros, how will I know if I have found the perfect man/woman/cyborg for me?”.
Worry not, gentle reader, for our science department is here to give you the answer to that question.
Imagine for a moment that, on a night out at the bar, you meet a girl/guy. You feel like you’ve never felt before the past week, and, whether it’s the alcohol thinking or not, you feel like you could really spend your life with them!
Not so fast, though. How will you know if they are right for you, or if you just have not met enough people to know that someone out there is even better?
This question has stumped scientists for millenia, but today we are here to give you the answer.
To make things easier, let’s transform the problem to something more intuitive. Let’s say that you have a sack full of envelopes, and each envelope has some money in it. Santa Claus quickly realises where he left the sack and comes back, telling you that that money is for all the good children. However, since you safeguarded the sack, he will let you pick one envelope. You can open as many as you want, but after you open an envelope you can either accept or decline it, and it will never be available to you again.
The envelopes here are potential mates, and the amount of money in them is how well you, personally, get along with them overall. The higher the amount, the better suited a person would be as your long-term partner.
The problem is, how do you know which envelope is worth keeping? Sure, the first one is for $100, but how do you know it’s not the smallest amount in the sack? Conversely, how do you know it’s not the largest?
Obviously, you need to sample a few times and get the overall feeling of the price ranges. How many times, though?
Well, statistically (and assuming a gaussian distribution), the first envelope you pick is likely to be somewhere around the 50th percentile. The second one, around 58. The third around 63 and so on. After 30 draws, you have gotten to 80.6. To get to 90, you’d have to go all the way up to 160 draws.
Of course, as you go higher the sums get rarer and rarer. If you drew 10 times and found what the sums are at the 73rd percentile and then drew once more and the sum was considerably larger (say, in the 95th percentile), you might want to stop, because you just got lucky. If you decided not to, you’d find that sort of sum again after around 500 draws.
The graph below shows the curve of expected maximal values for 30 draws:
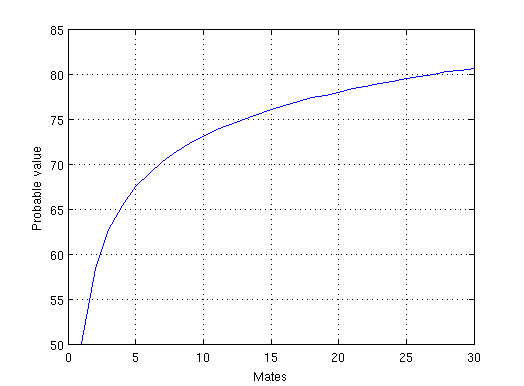
Since, however, evaluating a person takes so much longer, most people don’t have enough time to sample 500 times. You might be smart about it and extrapolate the percentiles of each value to see if they’re over 90, but that’s really not very practical, as it’s hard to rate people.
We do, though, see that it gets harder and harder to find good matches the more draws we make. In the second draw, the percentage jumps from 50% to 58%, a whole 8 points, while from the third to the fourth a mere
- By the time you get to ten draws, it’s a fraction of a percent. It would be wise for someone to stop at that point and decide that, since they’ve seen the 73rd percentile, they are going to pick the next person that is better or comparable to the best one of the 10 previous (i.e. the one at the 73rd percentile).
Unfortunately, there’s no hard-and-fast rule, but 10 draws seems to be a good number, as you’ve probably seen what the best of three quarters of the population looks like. The final decision is up to you, and take it with a grain of salt, because, as they say, “love is innumerate”.